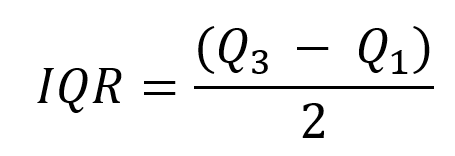The secret to getting machine learning to work effectively is in ensuring that the data we are using for training is as clean as possible and has any bias removed from it. When working with machine learning, we should be building in a generalised mode and to do this we need to understand what is happening inside our data. A common problem in machine learning which can throw your model off massively are outliers. In this blog, I want to take you through three different approaches that you can use to overcome the problem of outlier identification and in how you can resolve them.

There are 3 statistical methods to identify and remove outliers:

Standard Deviation (STD)
Median Absolute Deviation (MAD)
Interquartile Deviation (IQD)

Standard Deviation

The calculation for standard deviation looks intimidating but thankfully Spark has a built-in function for it already. In fact, it has two, ‘stddev_pop’ and ‘stddev_samp’. The difference between the two is very minor and one (‘stddev_pop’) should be used when calculation on the entire dataset or population. The other (‘stddev_samp’) should be used when run on a sample or subset of the data.

To use the standard deviation function to identify outliers, you should compare it to the mean. If the value is over a certain number of standard deviations away from the mean, it can be classed as an outlier. This certain number is called the threshold and often the default number is 3.

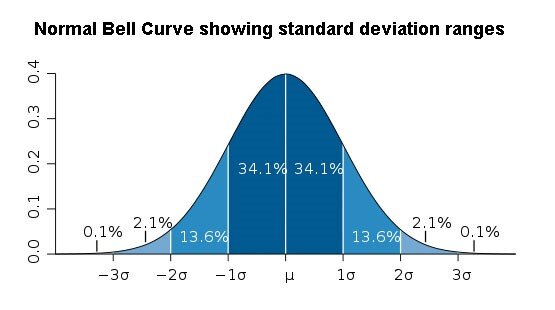
This calculation works on the basis that you have Gaussian distribution (a Bell curve). You will need to know the shape of your data to be able to identify outliers. Look at three standard deviations away from the mean in the Bell curve below:

Based on the image above, you can see that if you move 3 standard deviations away from the mean then we would expect a value to only appear over that threshold in 0.02% of the time.

Standard Deviation in Spark

import pyspark.sql.functions as F

stddevdf = (df.groupBy("genre").agg(F.stddev_pop("duration").alias("duration_std_pop"), F.avg("duration").alias("duration_avg")))

outliersremoved = df.join(stddevdf, "genre", "left").filter(F.abs(F.col("duration")-F.col("duration_avg")) <= (F.col("duration_std_pop")*3))

The one drawback of this method is that some outliers can fly under the radar. When the dataset contains extreme outliers, the standard deviation in increased, and the more minor outliers aren’t identified. Where your data does not conform to a gaussian distribution, for example, where you have a bimodal distribution, then you need to look at an alternative approach.

Median Absolute Deviation

To calculate Median Absolute Deviation (MAD) you need to calculate the difference between the value and the median. In simpler terms, you will need to calculate the median of the entire dataset, the difference between each value and this median, then take another median of all the differences.

In Spark you can use a SQL expression ‘percentile()’ to calculate any medians or quartiles in a dataframe. ‘percentile()’ expects a column and an array of percentiles to calculate (for median we can provide ‘array(0.5)’ because we want the 50% value ie median) and will return an array of results.

Like standard deviation, to use MAD to identify the outliers it needs to be a certain number of MAD’s away. This number is also referred to as the threshold and is defaulted to 3.

Median Absolute Deviation in Spark

MADdf = df.groupby('genre').agg(F.expr('percentile(duration, array(0.5))')[0].alias('duration_median')).join(df, "genre", "left").withColumn("duration_difference_median", F.abs(F.col('duration')-F.col('duration_median'))).groupby('genre', 'duration_median').agg(F.expr('percentile(duration_difference_median, array(0.5))')[0].alias('median_absolute_difference'))

outliersremoved = df.join(MADdf, "genre", "left").filter(F.abs(F.col("duration")-F.col("duration_median")) <= (F.col("mean_absolute_difference")*3))

This method is generally more effective than standard deviation but it suffers from the opposite problem as it can be too aggressive in identifying values as outliers even though they are not really extremely different. For an extreme example: if more than 50% of the data points have the same value, MAD is computed to be 0, so any value different from the residual median is classified as an outlier.

Interquartile Deviation

Interquartile Deviation uses the Interquartile Range (IQR) to classify outliers. The IQR is calculated simply as being the middle value between the lower and upper quartile of the data.

Like the median value, upper and lower quartiles can be calculated using ‘percentile()’. This time, however, instead of wanting the 50% percentile we want 25% and 75% percentiles for our lower and upper quartiles respectively.

An outlier will be classified as such if it is a certain amount of IQR’s away from the median value. This default threshold is 2.22, which is equivalent to 3 standard deviations or mads.

Interquartile Deviation in Spark

IQRdf = df.groupby('genre').agg(F.expr('percentile(duration, array(0.25))')[0].alias('lower_quartile'), F.expr('percentile(duration, array(0.75))')[0].alias('upper_quartile'), F.expr('percentile(duration, array(0.5))')[0].alias('duration_median')).withColumn("quartile_deviation", (F.col("upper_quartile") - F.col("lower_quartile"))/2)

outliersremoved = explodesplitdf.join(IQRdf, "genre", "left").filter(F.abs(F.col("duration")-F.col("duration_median")) >= (F.col("quartile_deviation")*2.2))

Compared the two methods above, this method is less influenced by extreme outliers like standard deviation but less sensitive to minor outliers like MAD. This means it can be used for both symmetric and asymmetric data.

The trick to managing outliers, is to really understand the shape of every feature in your data. Knowing the skew and kurtosis of each of your features will help make sure that you are able to accurately infer where outliers are potentially causing a problem.

Blog

Identifying Data Outliers in Apache Spark 3.0